[Algorithm] 너비 우선 탐색 & 다익스트라 알고리즘
in Algorithm
Elice Algorithm Code Challenge - Day 6 (너비 우선 탐색)
목차
너비 우선 탐색 (BFS)
BFS (Breadth First Search)
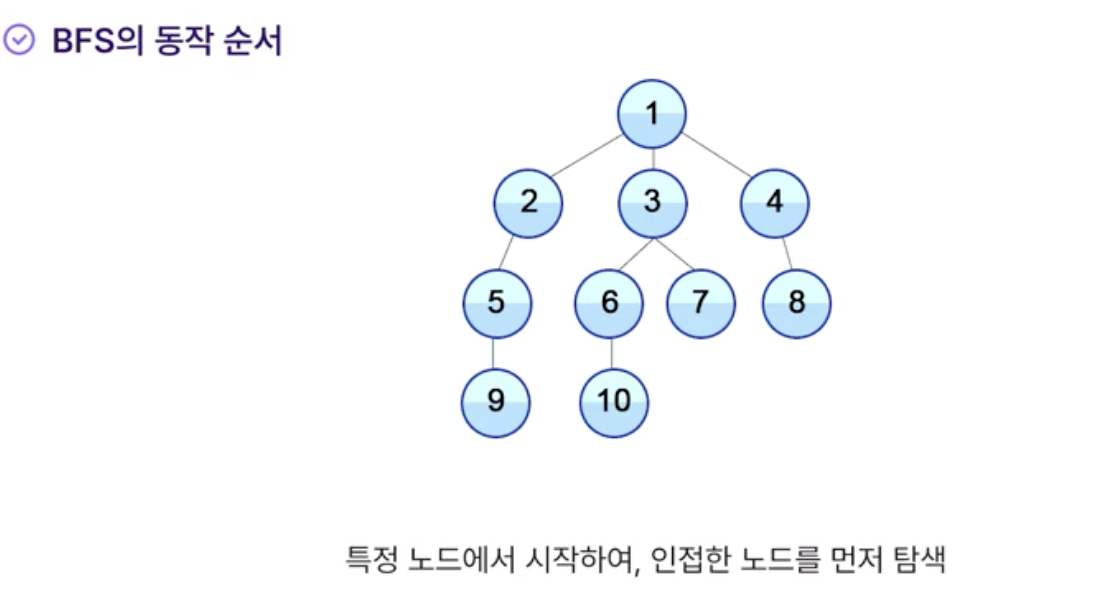
- 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
- 루트 노드 (혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용
BFS의 특징
- 재귀적으로 동작하는 DFS와 달리, BFS는 주로 큐(Queue) 사용
- 사이클이 있는 경우, 무한 루프에 빠지지 않도록 방문하는 방문 체크를 해주어야 함
- 물웅덩이에 돌멩이를 하나 던지면, 파동이 전체 방향으로 퍼져나가는 동심원의 형태로 탐색이 진행
BFS의 동작 순서
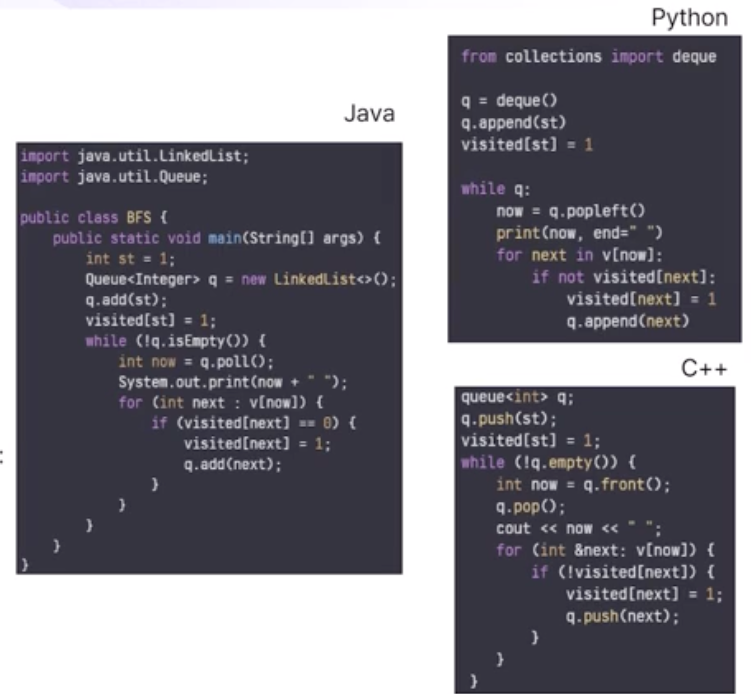
BFS의 구현
- 빈 큐 q 및 visited 배열 생성
- 시작 노드 ‘st’를 큐 q에 삽입
- 노드 ‘st’를 방문한 것으로 표시
- 큐 q가 비어있지 않은 동안 다음을 반복 :
- 큐의 맨 앞에서 요소를 꺼내 ‘now’에 저장
- 큐의 맨 앞의 요소를 제거
- ‘now’의 값을 출력하고 뒤에 공백을 붙임
- 노드 ‘now’의 인접 리스트 v에서 각 이웃 ‘next’에 대해
- 만약 ‘next’가 아직 방문하지 않은 노드인 경우 :
- 노드 ‘next’를 방문한 것으로 표시
- ‘next’를 큐 q에 넣음
- 만약 ‘next’가 아직 방문하지 않은 노드인 경우 :
BFS의 시간복잡도
- V : 정점(노드)의 수, E : 간선의 수
- 인접 리스트로 표현된 그래프
- O(V+E)
인접 행렬로 표현된 그래프
- O(V^2)
DFS와 BFS의 공통점과 차이점
공통점
- 그래프에서 시작 노드로부터 목적지 노드까지 도달하거니 특정 정보를 찾는 것이 목표
- 방문 기록을 체크해 이미 방문한 노드를 다시 방문하지 않게 하여 무한 루프 방지
- DFS, BFS 두 방식 모드 조건 내의 모든 노드를 검색한다는 점에서 시간 복잡도는 동일
차이점
- DFS는 주로 재귀로 구현하지만, BFS는 큐(queue) 자료구조를 활용하여 구현
- 일반적으로 DFS보다 BFS가 조금 더 빠르게 동작
- 동작 순서 상 DFS는 트리를 탐색할 때 자주 사용, BFS는 최단 경로 탐색에서 자주 사용
- DFS는 주로 재귀로 구현하지만, BFS는 큐(queue) 자료구조를 활용하여 구현
시간 복잡도
- 주어진 그래프의 구조와 시작 노드에 따라서 실제 시간 복잡도가 다를 수 있으며,
- 어떤 알고리즘이 더 효율적인지는 그래프의 형태와 알고리즘의 목적에 따라 달라짐
- 일반적으로 어떤 알고리즘을 선택할지는 문제의 특성과 요구사항에 따라 결정
다익스트라 (Dijkstra) 알고리즘
- 그래프 알고리즘
- 알고리즘을 사용하는 경우
- BFS 사용 시, 격자모양의 미로에서는 상하좌우 방향의 가중치가 모두 동일
- 현재 정점에서 이어진 간선들의 가중치가 모두 동일
- 하지만 가중치가 모두 일정하지 않다면 -> BFS를 사용할 수 없음
- BFS 사용 시, 격자모양의 미로에서는 상하좌우 방향의 가중치가 모두 동일
다익스트라 알고리즘 설명
- 한 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘
- 간선의 가중치가 양수일 때만 사용 가능
- 음수면 다익스트라가 아닌 테이크스트라 알고리즘 사용
- BFS와 유사하지만, 일반적인 큐가 아닌 우선순위 큐(Priority Queue)를 사용하여 비용이 가장 작은 간선부터 탐색한다는 차이점이 있음
- 우선순위 큐 (Priority Queue)
- 들어오는 순서에 상관 없이 우선 순위가 높은 데이터가 먼저 나가는 자료구조
- Heap을 이용해 구현하는 것이 가장 효율적
- 우선순위 큐 (Priority Queue)
- 그리디(Greedy) 알고리즘
- 매 단계에서 현재까지의 부분 해(solution)를 최적화하여 최종적으로 전체 문제의 최적 해를 찾아냄
다익스트라 알고리즘 동작 순서
- 출발 노드 선택
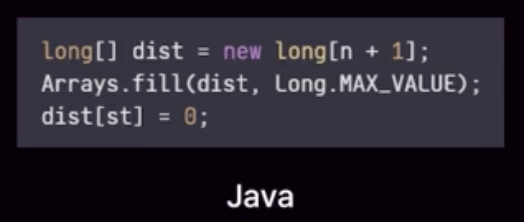
- 출발 노드로부터 각 노드까지의 최단 거리 배열 초기화
- 출발노드 거리는 0, 나머지 노드는 무한대(충분히 큰 값)로 설정
- 현재 노드 설정
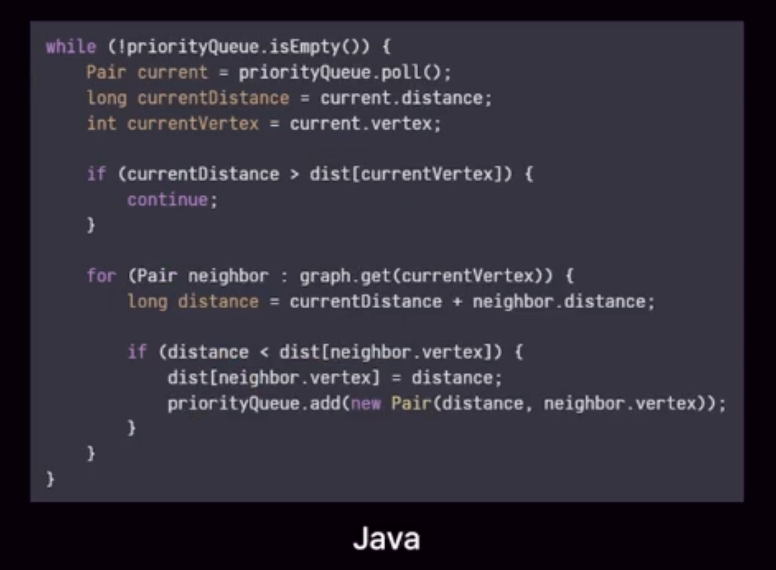
- 현재까지의 최단 거리가 확정된 노드 중 가장 가까운 노드 선택
- 이웃 노드 갱신
- 선택한 노드를 기준으로 해당 노드와 이웃한 노드들 간의 거리 갱신
- 모든 노드를 확인할 때까지 3,4단계 반복
- 핵심 아이디어
- 각 노드까지의 현재까지 알려진 최단 거리를 계속 갱신하며 출발 노드로부터 최단 경로를 찾는 것
- 비용이 가장 작은 간선부터 이어주기 위해 우선순위 큐를 사용한다.
다익스트라 알고리즘 시간 복잡도
- V : 정점(노드)의 수, E : 간선의 수
- O(ElogV)
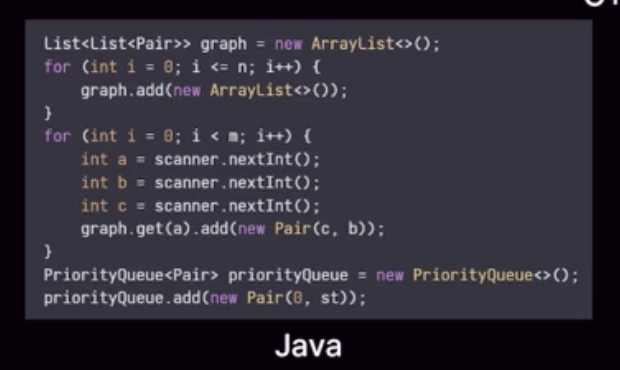
다익스트라 알고리즘의 구현
- 문제 예시
- 방향 그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로의 비용을 구하여라
- 첫째 줄에 정점의 개수와 간선의 개수가 입력됨
- 둘째 줄에는 시작 정점의 번호가 입력됨
- 셋째 줄부터 간선의 개수만큼의 줄에 걸쳐 (u,v,w)가 주어짐
- (u,v,w) -> u에서 v로 가는 양의 가중치 w인 간선 존재
- 구현 예시
- 출발 노드 선택
- 출발 노드로부터 각 노드까지의 최단 거리 배열 초기화
- 현재 노드 설정
- 이웃 노드 갱신
- 모든 노드 확인할 때까지 3,4단계 반복
- 출발 노드 선택