[Algorithm] 서로소 집합과 유니온 파인드

in Algorithm

Elice Algorithm Code Challenge - Day 9 (유니온 파인드)

트리와 관련된 용어들

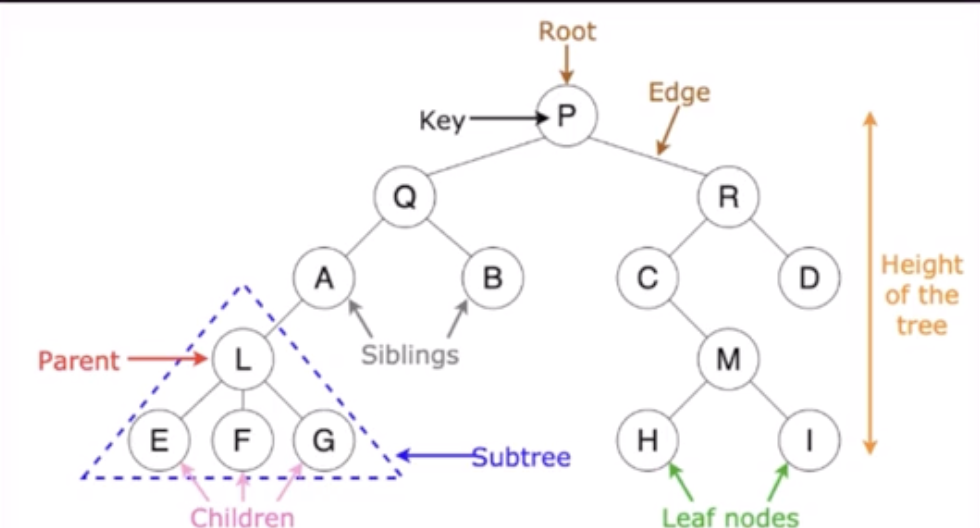
  • Full-width image
  • 루트 노드, 자식노드, 부모노드, 서브트리, 리프노드, 깊이
  • 이 이미지에서 깊이는 5
  • 이진트리
    • 자식 노드가 2개씩 있는 트리

서로소 집합

  • 서로 공통된 원소를 가지고 있지 않은 두 개 이상의 집합
  • 분리 집합 (Disjoint Set)이라고도 부름
  • 사용 용도
    • 서로 다른 원소들이 같은 집합에 속해있는지, 아닌지 판별할 때 사용
    • 사이클이 존재하는지 판별할때 사용
  • Union-Find 자료구조로 서로소 집합을 표현
    • 유니온 파인드가 다른 고급 알고리즘의 베이스가 됨 (Kruskal Algorithm)

유니온 파인드

유니온 파인드(Union-Find)의 자료구조

  • init, find, merge(union) 함수들의 형태로 보통 이루어짐
    • 함수명 고정 X
  1. init
  • 초기화 함수
  • Parent 배열에 대해 자신의 인덱스 값을 가지도록 초기화
    • 초기에 자신의 부모 노드는 자신이라는 의미
  •   void init() {
    for (int i = 1; i <= n; ++i) {
      parent[i] = i;
    }
  }
  1. find
  • 자신의 부모 노드를 찾는 함수
  • 재귀 함수로 구현됨
  • 자기 자신을 가리키는 인덱스 (루트 노드)를 찾을 때까지 반복
  •     int find_parent1(int x) {
      return x == parent[x] ? x : find_parent1(parent[x]);
    }

    int find_parent2(int x) {
      if (x == parent[x]) return x;
      else return parent[x] = find_parent2(parent[x]);
    }
    // memoization을 사용하는 2가 더 빠름
    ```
  1. merge
  • 두 노드를 하나의 집합으로 합치는 함수
    • y의 부모 노드는 x
  • find 함수를 같이 사용
  • if 문에서 x == y이면?
    • 사이클이 발생하는 경우이므로 제외
  •     void merge_parent(int x, int y) {
      int x = find_parent(x);
      int y = find_parent(y);

      if (x != y) parent[y] = x;
    }
    ```

유니온 파인드의 예시

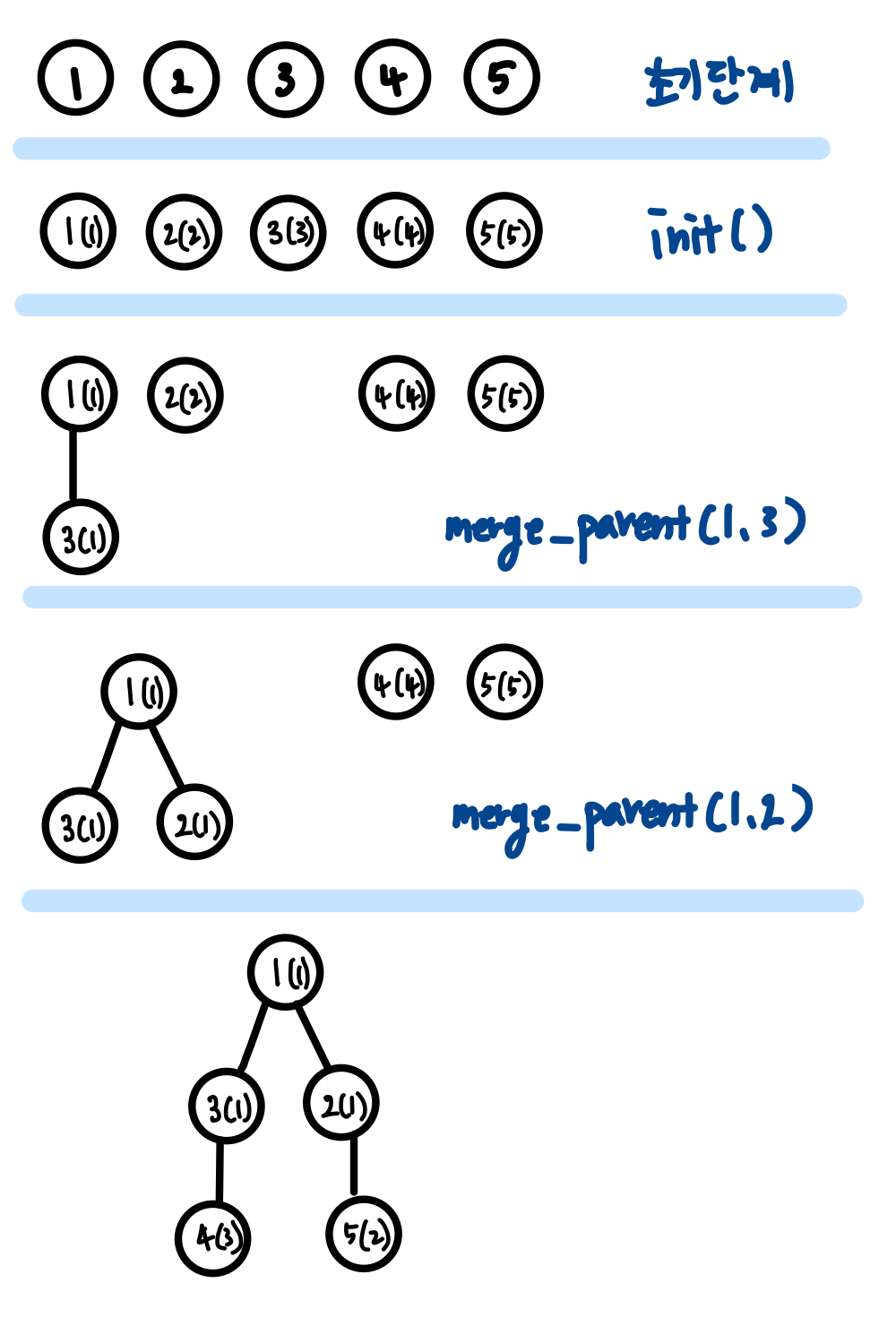
  • Full-width image
  • 최종적으로 오직 루트 노드만이 자기 자신을 가리키게 됨
    • 이러한 특서으로 루트 노드 찾을 수 있음